Here’s a problem (2.1.5, p. 23) from Lang’s “A Second Course in Calculus”:
In exercises 3 and 4, show that the velocity vector is perpendicular to the position vector.
For reference, exercise 3 is: (cos(t), sin(t)), and exercise 4 is (cos(3t), sin(3t)). If a velocity vector is perpendicular to a position vector, then the dot product of the position and velocity vectors has to be 0.
Let’s start with the position vector in exercise 3: (cos(t), sin(t)). The velocity vector of this position vector is the derivative of each term, or (-sin(t), cos(t)). Let’s take the dot product:
(cos(t))(-sin(t)) + (sin(t))(cos(t)) = -(sin(t)cos(t)) + (sin(t)cos(t) = 0
Thus, in exercise 3, the existence of a dot product of 0 confirms that the velocity vector is perpendicular to the position vector.
Now, for exercise 5, the position vector is (cos(3t), sin(3t)), and, therefore, the velocity vector is:
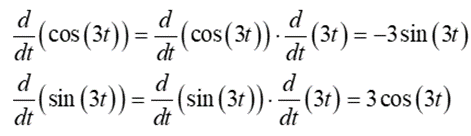
Therefore, the velocity vector of (cos(3t), sin(3t)) is (-3sin(3t), 3cos(3t)). Taking the dot product, we have:
(cos(3t))(-3sin(3t)) + (sin(3t)(3cos(3t)) =
-3(cos(3t))(sin(3t)) + 3(cos(3t)(sin(3t)) = 0
Thus, in exercise 5 also, the existence of a dot product of 0 confirms that the velocity vector is perpendicular to the position vector.
BridgeText can help you with all of your statistical analysis and mathematics needs.





