Position, Velocity, and Acceleration: A Worked Calculus Problem
Here’s a problem (4.1.87) from Larson et al.’s 9th edition of Calculus:
At the instant the traffic light turns green, a car that has been waiting at an intersection starts with a constant acceleration of 6 feet per second per second. At the same instant, a truck passing with a constant velocity of 30 feet per second passes the car. (a) How far beyond its starting point will the car pass the truck? (b) How fast will the car be traveling when it passes the truck?
Here's a handy way of setting up this problem:
Remember the acronym PVAD, or People View a Dance, for sequencing position, velocity, acceleration, and distance in differential calculus. To move up from P to V to A, you differentiate; to move back down this chain, you integrate. We begin by populating this table with what we know.
The intuition in this problem is to note that we are being asked, in part (a), when the position of the car and truck are equal. So we have to work backwards and complete the table in order to get position values for both vehicles:
Remind yourself that: 
. Note also that we are using t instead of x as the variable for time, but that doesn’t change the underlying logic. Start with a = 6 for the acceleration of the car. Note that 6 is the same is 6t0, with n = 0. Therefore, 
. Apply the same rule to integrate 6t: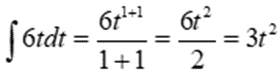 
. So, beginning with the acceleration of the car, which we knew, we worked backwards to velocity, then to position. You can apply the same rule of integration to get from the velocity (30) of the truck to its position, which is 30t. Now we can set up an equation as follows:
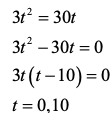
Here, the intuition is that the car and truck are level with each other when their positions are equal, which, as we can see, happens twice, at 0 seconds and 10 seconds. We are not interested in what happens at 0 seconds, so the answer is 10 seconds—but, again, note that we are asked where the vehicles will be when the car pulls ahead. Therefore, we have to plug 10 into t; note that 30t = 300 and 3t2 is also 300. Therefore, it is at 300 feet from the light that the car pulls ahead.
Part b asks us: How fast will the car be traveling when it passes the truck? ‘Fast’ means velocity in calculus terms. We already have the velocity function for the car, which is 6t. Thus, just plug 10 into t here, and, of course, 6(10) = 60. Therefore, the car’s speed will be 60 feet per second when it passes the truck.
BridgeText can help you with all of your statistical analysis and mathematics needs.
