Item Response Theory (IRT), often referred to as modern test theory, provides a framework for modeling the relationship between a test taker's latent ability and the probability of correctly answering test items. Unlike classical test theory, which focuses on overall test scores, IRT allows for the examination of individual test items, making it a powerful tool for test development and analysis.
Core Concepts of IRT
• Latent Trait or Ability: This is an unobservable characteristic or quality of an individual, often referred to as their "ability." In the context of an educational test, this could refer to a student's proficiency in a subject.
• Item Characteristic Curve (ICC): For each item in a test, there's a probabilistic curve (ICC) that represents the likelihood of a correct response based on the test taker's ability.
• Item Parameters: Each item is defined by specific parameters:
• Difficulty: Indicates the point on the ability scale where a student has a 50% chance of getting the item right. A higher difficulty value suggests that the item is harder.
• Discrimination: Measures how well an item differentiates between individuals of varying abilities. A high discrimination value means the item is very effective at distinguishing between high- and low-ability individuals.
Introducing the Mock Data
To understand IRT in practice, we've created a simulated dataset representing 20 students' answers to 20 test questions. In this dataset, a "0" indicates a wrong answer, while a "1" indicates a correct one. We've designed this data to exhibit certain patterns in difficulty and discrimination to illustrate the principles of IRT. You can run the following code in R:
# Step 1: Install and load necessary libraries
install.packages("ltm")
library(ltm)
# Step 2: Simulate the data
# Number of students and questions
n_students <- 20
n_questions <- 20
# Simulate student abilities from a normal distribution
student_abilities <- rnorm(n_students)
# Define item parameters
# Difficulty level for each question (higher values indicate more difficulty)
difficulty <- c(rep(1, 5), rep(0, 5), rep(-1, 5), rep(0, 5))
# Discrimination level for each question (higher values indicate better discrimination)
discrimination <- c(rep(2, 5), rep(1, 5), rep(1, 5), rep(2, 5))
# Simulate student responses
simulate_response <- function(student_ability, difficulty, discrimination) {
prob = exp(discrimination * (student_ability - difficulty)) /
(1 + exp(discrimination * (student_ability - difficulty)))
return(rbinom(1, 1, prob))
}
data_matrix <- matrix(0, n_students, n_questions)
for (i in 1:n_students) {
for (j in 1:n_questions) {
data_matrix[i, j] <- simulate_response(student_abilities[i], difficulty[j], discrimination[j])
}
}
# Step 3: Run IRT model
fit <- ltm(data_matrix ~ z1)
# Display the summary of the model
summary(fit)
Results
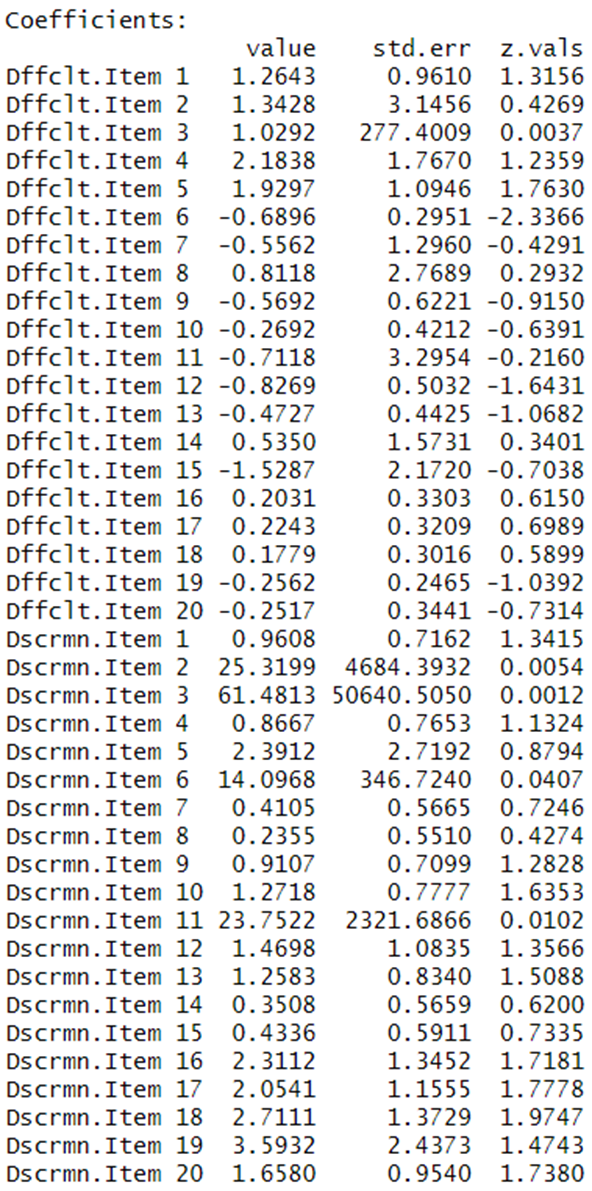
Discussion
Items like "Item 4" and "Item 5" have been found to be more challenging, with difficulty values of 2.1838 and 1.9297 respectively.
Conversely, items such as "Item 6", "Item 11", and "Item 12" appear to be among the easier questions based on their negative difficulty values.
Questions like "Item 19", "Item 18", and "Item 17" excel at distinguishing between students with different abilities, given their high discrimination values.
Some items, like "Item 8" and "Item 14", demonstrate low discrimination values, suggesting they may not be as effective in differentiating between high- and low-ability students.
Considerations: It's essential to account for the reliability of estimates. For instance, "Item 3" in our mock data exhibits very high standard errors, making its difficulty and discrimination estimates less reliable.
Conclusion
IRT provides a nuanced understanding of both the test as a whole and its individual items. Using IRT, educators and test developers can pinpoint which items are effective and which may need revision. Our mock data exercise illustrates these principles, emphasizing the importance of considering both the difficulty and discrimination parameters, as well as the reliability of these estimates. By leveraging IRT, we can aspire to develop better assessments that offer meaningful insights into student performance.
BridgeText can help you with all of your statistics needs.





